矩阵乘法

如果真的计算 ，那么他的时间复杂度是O(n³)，非常慢，代码如下

#include <cstdio>
#include <iostream>
using namespace std;
const int maxn = 999;
struct mat {
  double m[maxn][maxn];
};
mat a, b, c;
int l1, l2, l3;
void mul() {
  for (int i = 0; i < l1; i++)
    for (int j = 0; j < l3; j++) {
      for (int k = 0; k < l2; k++) {
        c.m[i][j] += a.m[i][k] * b.m[k][j];
      }
    }
}
int main() {
  memset(c.m, 0, sizeof(c.m));
  cin >> l1 >> l2 >> l3;
  for (int i = 0; i < l1; i++) {
    for (int j = 0; j < l2; j++) {
      cin >> a.m[i][j];
    }
  }
  for (int i = 0; i < l2; i++) {
    for (int j = 0; j < l3; j++) {
      cin >> b.m[i][j];
    }
  }
  mul();
  for (int i = 0; i < l1; i++) {
    for (int j = 0; j < l3; j++) {
      cout << c.m[i][j] << " ";
    }
    cout << endl;
  }
}

矩阵快速幂

矩阵快速幂的核心代码是这样的

while (n) {
    if (n & 1){
        ans = multi(ans, base);
    }
    base = multi(base, base);
    n >>= 1;
}

其中，n & 1是取n的二进制代码的最后一位，n >>= 1是将n做位运算，将n右移一位，左侧补零。现在详细说一下矩阵快速幂算法：

为什么需要快速幂？

对于幂运算，比如2的100次方。

常规的算法就是要用2一直乘下去，代码效率十分低，耗费时间复杂度非常高。

那什么是快速幂？

快速幂算法就是为了解决矩阵相乘好费时间的问题，当22=4之后，就可以利用44区代替222*2，这样一来就有了很大的时间节约。

时间复杂度差多少？

传统的幂运算是O(N),而快速幂算法则是O(log₂N)。速度相对有很大的提升。

那怎么实现呢？

利用了强大的位运算。

那什么是矩阵快速幂？

矩阵快速幂就是矩阵的快速幂，为什么要单独拿出来讲矩阵呢？矩阵的普速算法的时间复杂度是 $O(mn^3)$ 这是相当慢的，而快速幂的算法是可以将复杂度降到$O(n^3logM)$这就有了很大的优化，因为一般M是远远大于n的。

矩阵快速幂与斐波那契

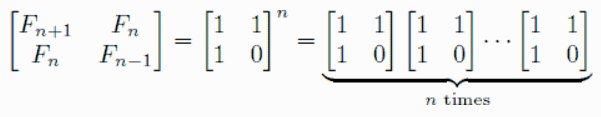
这就是和斐波那契数列的关系，斐波那契数列直接算法耗时巨大，而使用矩阵快速幂可以大大降低时间复杂度。

对于类似斐波那契的数列给出如下的计算方法：

这样，就可以利用矩阵快速幂的方式计算出所需了。

剑指offer && Leetcode 509

题解

先看一道题：POJ 3070

看一道题poj3070

[https://vjudge.net/problem/POJ-3070](https://vjudge.net/problem/POJ-3070 /h)

代码如下 利用了矩阵快速幂

#include <cstdio>
#include <iostream>
using namespace std;
const int MOD = 10000;
struct matrix {
  int m[2][2];
} ans, base;
matrix multi(matrix a, matrix b) {
  matrix tmp;
  for (int i = 0; i < 2; i++) {
    for (int j = 0; j < 2; j++) {
      tmp.m[i][j] = 0;
      for (int k = 0; k < 2; k++) {
        tmp.m[i][j] = (tmp.m[i][j] + a.m[i][k] * b.m[k][j]) % MOD;
      }
    }
  }
  return tmp;
}
int fast_mod(int n) {
  if (n == -1) return 0;
  base.m[0][0] = base.m[0][1] = base.m[1][0] = 1;
  base.m[1][1] = 0;
  ans.m[0][0] = ans.m[1][1] = 1;
  ans.m[1][0] = ans.m[0][1] = 0;
  while (n) {
    if (n & 1) {
      ans = multi(ans, base);
    }
    base = multi(base, base);
    n >>= 1;
  }
  return ans.m[0][0];
}
int main() {
  int n;
  while (scanf("%d", &n) && (n + 1)) {
    printf("%d\n", fast_mod(n - 1));
  }
  return 0;
}