Manacher算法：快速寻找最长回文串

0. 一个极简的Manacher算法例子

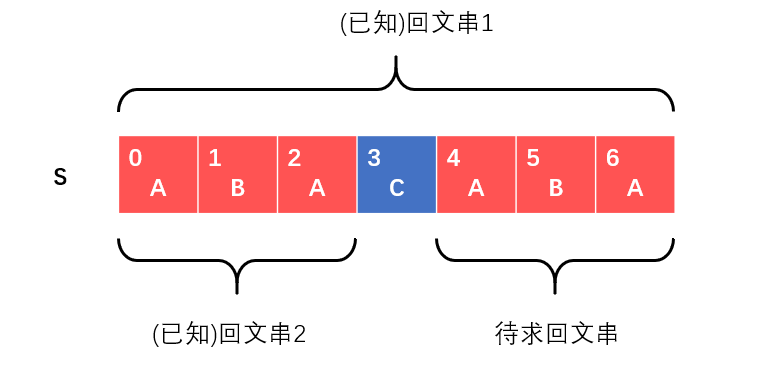
回文串是指中心对称的字符串。对于上面这个字符串$S$，如果我们想求以$S[5]$为中心的回文串，根据回文串1可知：回文串2和待求回文串是对称的。因此待求回文串的宽度与回文串2一致，即$S[4] - S[6]$。这就是Manacher算法的一个（并不严谨的）的简单例子。

如果想详细了解Manacher算法，还请看后文。

1. 中心拓展法计算最长回文串

Manacher算法是一种能够快速寻找回文串的方法。在讲Manacher之前，首先看一个问题Leetcode 5. 最长回文子串 (opens new window)：

问题描述：

给定一个字符串 s，找到 s 中最长的回文子串。你可以假设 s 的最大长度为 1000。

示例 1：

输入: "babad"
输出: "bab"
注意: "aba" 也是一个有效答案。
示例 2：

输入: "cbbd"
输出: "bb"

类似这种问题，对于任意一个的字符串，问该字符串中最长（或全部）的回文串（或最长的长度）。

解决这类问题的最常规的方法就是中心拓展法。中心拓展法的思路很简单：从一个字符或者两个相同字符（称为回文中心）开始向两侧拓展，直到出现两端的字符不同，那么当前的字符串就是以该回文中心为中心的最长回文串。

中心拓展法唯一需要注意的是，最终回文串的长度可能是奇数，也可能是偶数，因此中心也存在两种，一种是以当前点为中心（对应奇数长度），另一种是以当前点和下一个点为中心（对应偶数长度）。

拓展函数的代码如下：

pair<int, int> expandAroundCenter(string& s, int left, int right) {
  while (left >= 0 && right < s.size() && s[left] == s[right]) {
    --left;
    ++right;
  }
  return {left + 1, right - 1};
}

需要注意的是，上面这个函数并不会主动寻找两种中心，而是需要调用的时候用两次：

for (int i = 0; i < s.size() - 1; ++i) {
  auto [left1, right1] = expandAroundCenter(s, i, i);
  auto [left2, right2] = expandAroundCenter(s, i, i + 1);
  //接着判断哪个最大，或者维护最大长度
}

中心拓展法的时间复杂度是$O(N^2)$,$N$是字符串的长度。空间复杂度是$O(1)$，即无需额外空间。

2. Manacher算法

我们仔细观察中心拓展法就可以发现，中间存在很多反复的判断，直觉上造成了一定的浪费。Manacher算法正是通过一个简单的方法利用了前面已经判断完的回文串的信息，来降低复杂度，一举将$O(N^2)$降低到了$O(N)$，不过这种信息需要存储，也就是需要一定的空间代价，空间复杂度也从$O(1)$上升到了$O(N)$。

Manacher算法的核心是利用已知回文串的中心对称性，对未知中心拓展进行初始化，避免所有的中心拓展都从中心开始。

2.1 直觉上的过程

首先给出一个笼统的过程描述：给出一个字符串，假设我们准备寻找以$s[i]$为中心的回文串时，按照中心拓展的思想，需要从$s[i]$开始寻找。但是如果在$s[i]$左侧的，以$s[(i+j)/2]$为中心的回文串（即下图的“当前回文串”）已知，那么可以根据这个串的对称性，发现以$s[i]$和以$s[j]$中心的回文串是对称的，而以j为中心的回文串目前是已知的。因此，可以把以$s[j]$为中心的长度$d[j]$作为以$s[i]$为中心的回文串的长度$d[i]$,（即$d[i] = d[j]$），在此基础上再进行中心拓展，避免了每一个字符串都从零开始慢慢寻找。这就是Manacher算法的核心思想。

2.2 具体实现

理解大体的过程后，具体的实现需要维护两个东西来达到节约计算的目的：

• 一个是以每个字符为中心的最大回文半径d[i]（半径是否包括中心点可以自己规定，为了代码书写方便，此处不包括中心点）（它导致了空间复杂度的上升）
• 一个是所有已知回文串能达到的右侧最远的位置max_r，以及对应的回文串中心max_center

Manacher算法开始时就是普通的中心拓展法。不同的是，每次中心拓展前都要检验当前的字符是否被覆盖在max_center到max_r的范围内，如果在的话就要把开始拓展的位置进行初始化，再进行中心拓展。否则直接进行中心拓展。最后记得要更新所需要记录的值。

这里有一个需要注意的点，如果我们找到的对应回文串$d[j]$的范围超过了j - max_l（这里的max_l是右侧最远回文串的左端点，即max_l = 2*max_center - max_r），则不能把d[j]直接赋值给它，因为我们不知道超出右侧范围后的串的内容。这时候用来初始化的不应该是d[j]，而是j - l。

最后，还有一个重要的预处理技巧，因为存在奇数串和偶数串，为了容易处理，可以把原串的间隙（包括最左端和最右端）插入‘#’，例如[abcd]就变成[#a#b#c#d#]，这样操作后，无论怎样，串都是奇数个数，而中心点也只剩一个，上述的操作实现就不必再考虑两种情况了。

2.3 例题

最后还是以5. 最长回文子串 (opens new window)这个经典题为例子，本题是使用Manacher算法的模板题，下面给出实现代码：

时间复杂度：$O(N)$

空间复杂度：$O(N)$

class Solution {
 public:
  // 中心拓展
  pair<int, int> expandAroundCenter(string &s, int left, int right) {
    while (left >= 0 && right < s.size() && s[left] == s[right]) {
      --left;
      ++right;
    }
    return {left + 1, right - 1};
  }
  // 字符串预处理
  string createString(string &s) {
    string new_s = "#";
    for (auto &x : s) {
      new_s += x;
      new_s += '#';
    }
    return new_s;
  }

  // main function
  string longestPalindrome(string s) {
    string new_s = createString(s);
    int n = new_s.size();
    vector<int> d(n + 1, 0);
    int max_ceter = -1, max_r = -1;

    for (int i = 0; i < n; ++i) {
      int start_right = i;
      int start_left = i;
      // Manacher的核心：拓展前的初始化
      if (i < max_r) {
        // max_l是max_r关于max_center的对称点
        auto max_l = 2 * max_ceter - max_r;
        // j是i关于max_center的对称点
        auto j = 2 * max_ceter - i;
        // 比较左边界max_l和d[j]，防止超出max_l
        auto temp_r = d[j] < j - max_l ? d[j] : j - max_l;
        // 初始化拓展位置
        start_right = i + temp_r;
        start_left = i - temp_r;
      }
      auto [left, right] = expandAroundCenter(new_s, start_left, start_right);
      // 维护与更新
      d[i] = (right - left) / 2;
      if (right > max_r) {
        max_r = right;
        max_ceter = i;
      }
    }
    // 返回问题所需结果，根据问题的不同而变化
    int max_index = 0;
    for (int i = 0; i < n + 1; ++i) {
      if (d[i] > d[max_index]) max_index = i;
    }
    return s.substr(max_index / 2 - d[max_index] / 2, d[max_index]);
  }
};

看起来代码长，但是如果理解了关键点其实很简单。

参考

【1】https://zhuanlan.zhihu.com/p/288756227

【2】https://leetcode-cn.com/problems/longest-palindromic-substring/solution/zui-chang-hui-wen-zi-chuan-by-leetcode-solution/