题目列表

84. 柱状图中最大的矩形 (opens new window)

85. 最大矩形 (opens new window)

496

739

503

901

以下列出了单调栈的问题，供大家参考。

序号 题目 题解 1 42. 接雨水（困难） 暴力解法、优化、双指针、单调栈 2 739. 每日温度（中等） 暴力解法 + 单调栈 3 496. 下一个更大元素 I（简单） 暴力解法、单调栈 4 316. 去除重复字母（困难） 栈 + 哨兵技巧（Java、C++、Python） 5 901. 股票价格跨度（中等） 「力扣」第 901 题：股票价格跨度（单调栈） 6 402. 移掉K位数字 7 581. 最短无序连续子数组 这里感谢 @chwma 朋友提供资料。

作者：liweiwei1419 链接：https://leetcode-cn.com/problems/largest-rectangle-in-histogram/solution/bao-li-jie-fa-zhan-by-liweiwei1419/ 来源：力扣（LeetCode） 著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。

Leetcode 84 柱状图中最大的矩形

题目：

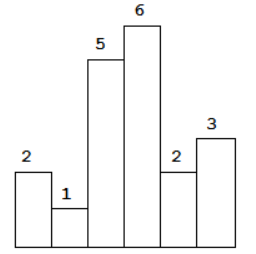
给定 n 个非负整数，用来表示柱状图中各个柱子的高度。每个柱子彼此相邻，且宽度为 1。

求在该柱状图中，能够勾勒出来的矩形的最大面积。

以上是柱状图的示例，其中每个柱子的宽度为 1，给定的高度为 [2,1,5,6,2,3]。

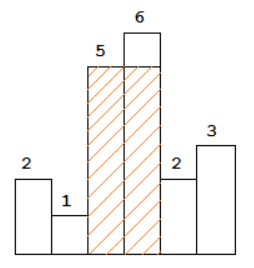
图中阴影部分为所能勾勒出的最大矩形面积，其面积为 10 个单位。

示例:

输入: [2,1,5,6,2,3] 输出: 10

分析：

思路是这样，对于每一个柱子，我们以该柱子为最终高度的范围，是该柱子左右两侧“第一个比该柱子矮的柱子”中间的长度。这个表述恰好就是单调栈所能解决的。也就是说，我们要求输入数组中每一个数字左侧第一个比自己小的值和右侧第一个比自己小的值。根据我们在理论篇中的结论，这里很容易想到解法。

我们新建一个left和一个right数组来存储每个元素左侧和右侧第一个比自己小的值的下标。由于找比自己小的值，因此使用单调递增栈。

直接来想，我们可以通过两次遍历，第一次找左侧第一个比自己小的值，第二次找右侧第一个比自己小的值。但是其实完全可以把两次操作合并成一次遍历，分别在单调栈push和pop的时候更新left和right。

接着再遍历一遍，对下标为i的每个值，只需要根据已有的left和right求出width，再乘以height[i]，就可以得到当前的面积。比较所有面积就可得到最终的答案。

这里有一个问题，那就是对于左侧没有更小的值（以及右侧没有更小的值）这种情况时，需要单独考虑width的计算。有一个巧妙的办法可以解决这个问题：在height数组的前后各插入一个0，这样就能保证所有的值都有比自己小的那个了。对于width的计算也变得更加简单。

时间复杂度：O(N)

空间复杂度：O(N)

代码：

class Solution {
public:
    int largestRectangleArea(vector<int>& heights) {
        heights.insert(heights.begin(), 0);
        heights.push_back(0);
        int n = heights.size();
        auto left = vector(n, -1);
        auto right = vector(n, -1);
        stack<int> mono_st;
        for (int i = 0 ; i < n ; ++i){
            while (!mono_st.empty() && heights[i] < heights[mono_st.top()]){
                right[mono_st.top()] = i;
                mono_st.pop();
            }
            if(!mono_st.empty()) left[i] = mono_st.top();
            mono_st.push(i);
        }

        int ret = INT_MIN;
        for(int i = 0 ; i < n ; ++i){
            auto area = (right[i] - left[i] - 1) * heights[i];
            if(ret < area)  ret = area;
        }
        return ret;
    }
};

Leetcode 85 最大矩形

参考

【1】

【2】https://leetcode-cn.com/problems/largest-rectangle-in-histogram/solution/zhu-zhuang-tu-zhong-zui-da-de-ju-xing-by-leetcode-/