LSTM与GRU
LSTM与GRU
# 1. LSTM
# 1.1 网络的大致结构与设计思路
循环神经网络的反向传播公式为 $$ \delta_k^T = \delta_k^T \prod_{i=k}^{t-1}diag[f^{'}(net_i)]W $$ 当$\delta_k^T$从t时刻传播到k时刻,$\delta_k^T$的上界可以表示为: $$ |\delta_k^T| \leq |\delta_k^T| \prod_{i=k}^{t-1}|diag[f^{'}(net_i)]| |W| \ \leq |\delta_k^T|(\beta_f\beta_W)^{t-k} $$ 从上式可以看出,当$t-k$非常大时(长时间跨度),$\beta_f\beta_W$必须尽可能贴近于1,如果小于1就会出现梯度消失。
当出现梯度消失时,反向传播过程中的误差就无法长距离的传递,这回对网络训练带来极大的难度。
为了解决这个问题,才出现了LSTM。
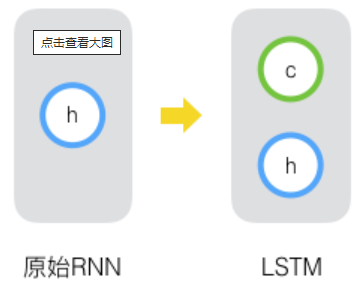
LSTM解决梯度消失的思路就是:增加一个状态c来保存长期的状态,并设计一个控制c的方法。
大致的结构就是下面这样:
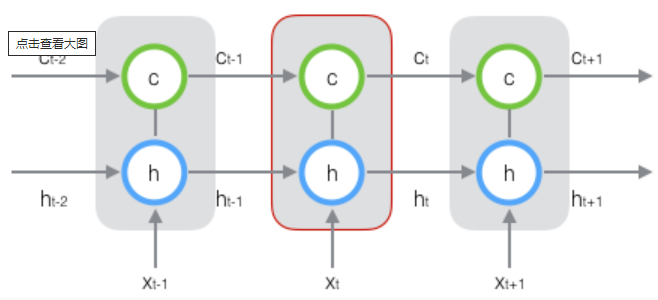
符号说明:
- $x_t$输入向量
- $h_t$短期状态
- $c_t$长期状态
# 1.2 网络中“门”的概念
门实际上就是一层全连接层,它的输入是一个向量,输出是一个0到1之间的实数向量。即 $$ g(x) = \sigma(Wx + b) $$ 其中,$b$是偏置项,$x$是输入,$W$是权重矩阵,$\sigma(*)$是sigmoid函数,它的值域是(0,1).
# 1.2.1 遗忘门、 输入门与输出门
· 称控制长期状态单元的门为遗忘门(forget gate),它决定了上一刻的状态单元$c_{t-1}$有多少保留到了当前的$c_t$。
· 称控制$x_t$有多少保存到$c_t$的门为输入门,
· 称控制$c_t$有多少输出到当前输出值$h_t$的门为输出门。
# 1.3 LSTM最终的网络结构(前向传播)
首先,LSTM是一个循环神经网络,它首先将上次的输出与这次的输入两个向量组合起来,即$[h_{t-1}, x_t]$,作为各个门的输入。
# 1.3.1 遗忘门的构造
$$ f_t = \sigma(W_f [h_{t-1}, x_t] + b_f) $$
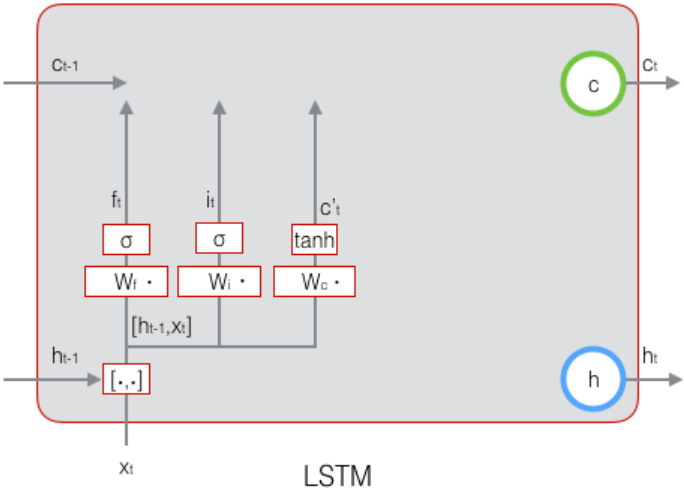
这首先构成了一个上面提到的门,$W_f$是遗忘门的权重矩阵,$b_f$是偏置项,这些在后面的输入门与输出门是类似的含义,不再赘述。此时的结构图:
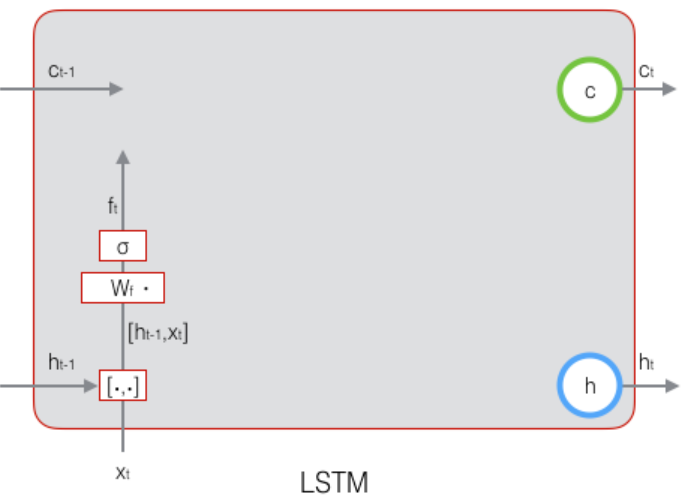
# 1.3.2 输入门的构造
公式如下: $$ i_t = \sigma(W_i [h_{t-1}, x_t] + b_i) $$ 这里再强调一下,输入门的目的是表达输入$x_t$有多少保存到了长期状态$c_t$中,但是现在还看不出来,因为最终的线没有连上,如下图。
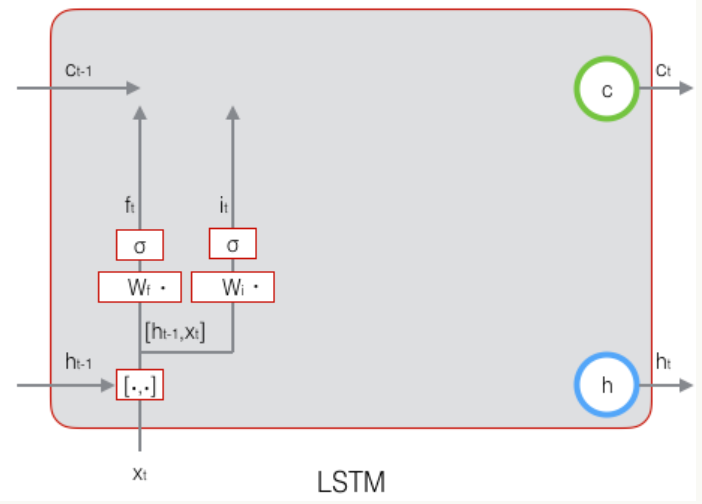
# 1.3.3 输入单元的构造
$$ \tilde c_t = tanh(W_c [h_{t-1}, x_t] + b_c) $$
输出门想表达的是$c_t$有多少从本层的结果$h_t$中输出了(也暂时看不出来,后面没有连上),如下图。
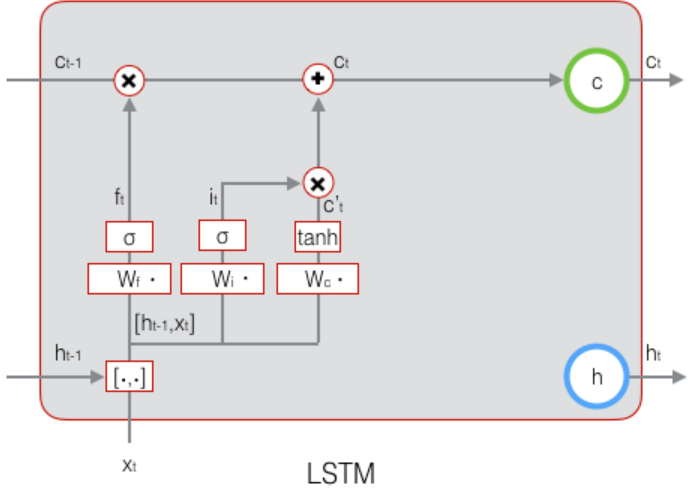
# 1.3.4 $c_t$的计算
$$ c_t = f_t \circ c_{t-1} + i_t \circ \tilde c_t $$
这里谁是向量??
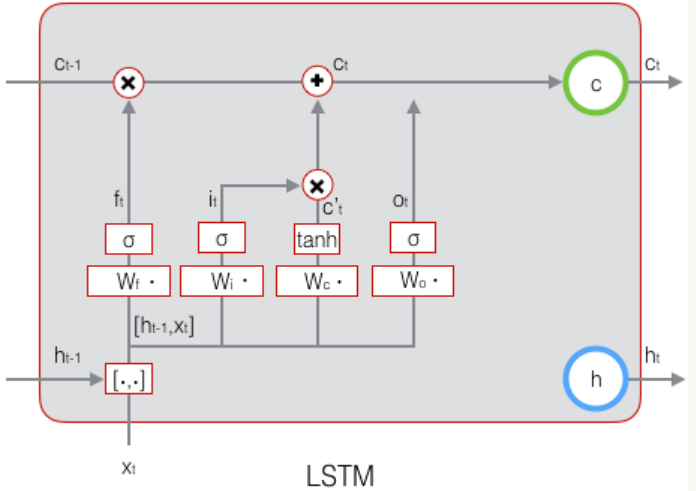
# 1.3.5 输出门的构造
$$ o_t = \sigma(W_o [h_{t-1}, x_t] + b_o) $$
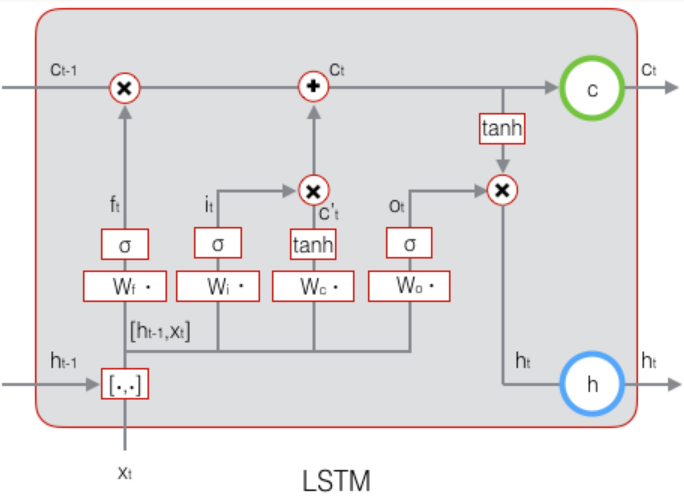
# 1.3.6 最终输出
$$ \mathrm{h}_t = \mathbf{o}_t\circ \tanh(\mathbf{c}_t) $$
# 1.4 LSTM的训练
# 2. GRU
# 参考
【1】《动手学深度学习》:面向中文读者、能运行、可讨论 (d2l.ai) (opens new window)