KMP与AC自动机

KMP算法

对于KMP的讲解，我认为如何更好地理解和掌握 KMP 算法? - 阮行止的回答 - 知乎 (opens new window)这篇回答的讲解已经非常细致了，没有必要对这种教程反复造轮子。这篇回答中只有对于next快速构建的一些部分不是很清晰。因此，下面一方面以笔记的性质记录我的理解，另一方面重述关于next构建的部分。

1.1 KMP的直觉过程

借用上面教程中的图进行一下说明。下面的图描述的是：从主串S中寻找模式串P的匹配过程。

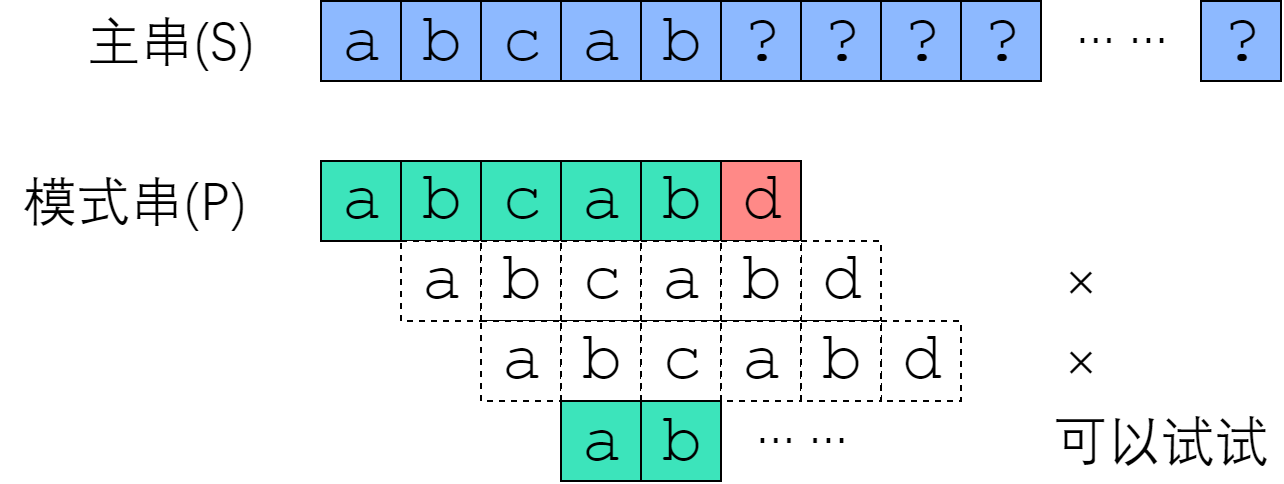
KMP整个过程的核心是利用已有的信息，对失配后的模式串进行“修正”（这里非常像Manacher算法）。这里的“修正”是个很抽象的词。在上面的图中，模式串的第一次匹配到最后一个字母‘d’时，发现了错误，即当前不能再匹配下去了，因此需要向后移位一格，再匹配。第二次匹配时第一个字母就错了，再移位一格。第三次第一个字母也不对，再移位一格。终于到了第四次，第一个字母能进行下去了，幸运的是第二个也能继续下去，之后就可以继续匹配第三个了。

这个过程可以发现一个特点，即对于主串来说，当前所指向的字符(即index_s)是不会往回走的，即一直是向后移动的**。失配后需要重新调整的只有指向模式串的index_p**。这在对KMP直觉的理解上是很重要的一点。

那么刚才提到的**“修正”指的是什么？其实就是从某一次匹配出错，利用某些信息直接跳过“连第一个字母都匹配不上”的状态，进入一定可以继续匹配**的过程。这个说法很不严谨，但是可以在一定程度上理解算法在做什么。对于这个过程，之前提到的教程的描述如下：

有些趟字符串比较是有可能会成功的；有些则毫无可能。我们刚刚提到过，优化 Brute-Force 的路线是“尽量减少比较的趟数”，而如果我们跳过那些绝不可能成功的字符串比较，则可以希望复杂度降低到能接受的范围。

这个过程究竟利用了什么信息，我觉得可以按下面的思路捋一下：

1. 模式串本身是蕴含一定信息的，比如第一个字母和第二个字母如果不一样，那么后移一位是一定没有意义的。
2. 如果当前S和P刚刚失配，意味着在这个字符前面的所有字符是“匹配的”
3. 如果存在2中的匹配，那么就可以把模式串本身的信息传递给了主串S

到这里，意思就很明确了。我们可以构建一个next，然后借用next中对前后缀的匹配关系，快速定位失配后的下一个index_p应该指向哪里。

就像下图：我们在匹配模式串的6和主串的6时出现了错误，那么这意味着主串和模式串的[0-5]是相同的。根据模式串自身携带的信息，我们知道模式串的[0-1]和[4-5]是相同的。根据前面匹配的特性，我们知道主串中的[0-1]和[4-5]也是相同的。因此下一次匹配时，我们可以让模式串的[0-1]和主串的[4-5]对齐，直接从主串的index_s = 6和模式串的index_p = 2开始比较，就可以继续了。值得注意的是，在从上次匹配到下次匹配的过程中，指向主串的index_s始终是没有变的，需要修正的，只有模式串的index_p。

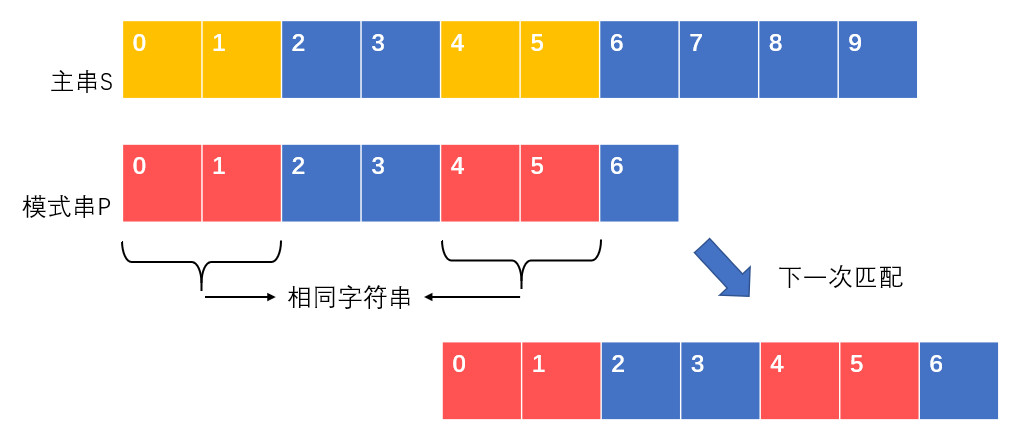
前面所有过程都是出于从直觉上理解KMP在做什么，而其中的思路，为什么这么做，next信息是什么，为什么需要next信息，在前面大佬的回答如何更好地理解和掌握 KMP 算法? - 阮行止的回答 - 知乎 (opens new window)中讲的非常清楚。

1.2 next的快速构建

在谈next的构建之前，必须强调的是next存储的是前后缀相同的最大“数量”，而非数组下标。而且定特别定义next[0] = 0。

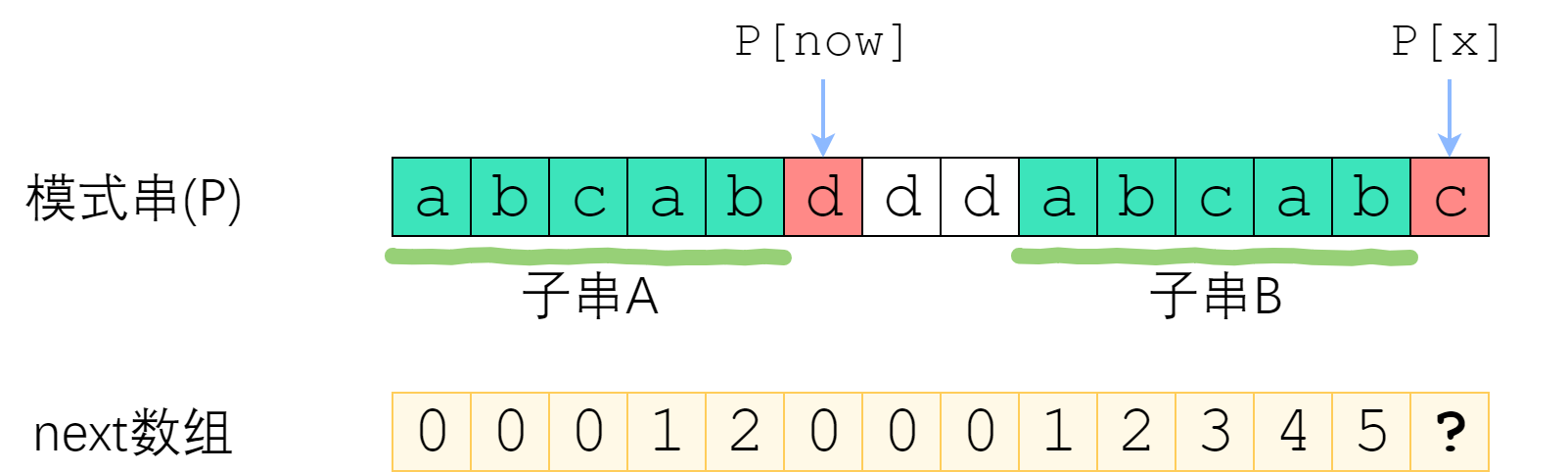
这里还是借用大佬的例子（我觉得他举的例子很好）

当我们的p[x]和p[now]出现不匹配时，这里next[x]不能继续增加。因此需要把now回调才能继续匹配。

这里最重要的一点是，虽然p[x]和p[now]失配了，但是这意味着子串A和子串B是完全匹配的。

我们要调整now来重新寻找对应。而调整now实际上就是要找子串A的前缀和子串B的后缀到底能重合多少（最大重合数量）。因为子串A和子串B是完全匹配的，因此我们要找的就是子串A的前缀和子串A的后缀最大重合多少（相当于把子串B的后缀变成子串A的后缀，因为他俩完全匹配），而这个问题的答案，就是next[now - 1]。

如果明白了这个过程，再去看前面大佬的题解，那就很明晰了。

1.3 KMP的C++实现

#include <iostream>
#include <string>
#include <vector>
using namespace std;

// KMP类： 实现了KMP的主要功能：
// - 构建next串
// - 匹配
class KMP {
  string s;
  string pattern;

 public:
  KMP(const string &s, const string &pattern) : s(s), pattern(pattern) {}

  // 构建next信息
  // 需要明确的是，next存储的是前缀与后缀最大相同的“个数”，而不是下标
  vector<int> buildNext(const string &s) {
    int n = s.size();
    vector<int> next(n, 0);
    int index = 1;
    int now = 0;

    while (index < n) {
      if (s[index] == s[now]) {
        //这里是一个非常重要的细节，先让now增，再给next[index]赋值，再增加index。顺序不可乱
        ++now;
        next[index] = now;
        ++index;
      } else if (now != 0) {
        now = next[now - 1];
      } else {
        next[index] = 0;
        ++index;
      }
    }
    return next;
  }

  // 寻找与匹配
  bool find() {
    auto next = buildNext(pattern);
    int n = s.size();
    int index_s = 0;
    int index_p = 0;

    // 输出当前任务的信息：
    printInfo(next);

    while (index_s < n) {
      if (s[index_s] == pattern[index_p]) {
        ++index_p;
        ++index_s;
      } else if (index_p != 0) {
        index_p = next[index_p - 1];
      } else {
        ++index_s;
      }

      if (index_p == pattern.size()) {
        cout << "s[" << index_s - pattern.size() << ", " << index_s - 1
             << "] = pattern" << endl;
        return true;
      }
    }
    return false;
  }

  void printInfo(const vector<int> &next) {
    cout << "s = " << s << endl;
    cout << "    ";
    for (int i = 0; i < s.size(); ++i) {
      cout << i % 10;
    }
    cout << endl;

    cout << "pattern = " << pattern << endl;

    cout << "next = ";
    for (auto &x : next) {
      cout << x;
    }
    cout << endl;
  }
};

int main() {
  // 简单验证
  string s = "abcddddabcddabxcddddabxcddddxabx";
  string pattern = "abxcddddxabx";
  KMP k(s, pattern);
  cout << k.find() << endl;
  cout << endl;

  string mode2 = "abxcddddxabxp";
  KMP k2(s, mode2);
  cout << k2.find() << endl;
  cout << endl;

  string s3 = "ababaabaabac";
  string mode3 = "abaabac";
  KMP k3(s3, mode3);
  cout << k3.find() << endl;

  string s4 = "aabaaabaaac";
  string mode4 = "aabaaac";
  KMP k4(s4, mode4);
  cout << k4.find() << endl;

  return 0;
}

AC自动机